| COS 126
Global Sequence Alignment |
Programming Assignment |
website
This assignment allows optional partnering. If you choose to do this, you must follow the pair programming guidelines. Please click the link and review them before you begin. Your partner can be from another precept (but ISC students may only partner with other ISC students). Please note that writing code with a partner without following the pair programming instructions is a violation of the course collaboration policy. All writing of code, comments, analysis and uploading to the dropbox should be done together from start to finish. If you come to office hours alone, you can get advice, but you may not change any code until both partners are together.
Write a program to compute the optimal sequence alignment of two DNA strings. This program will introduce you to the field of computational biology in which computers are used to do research on biological systems. Further, you will be introduced to a powerful algorithmic design paradigm known as dynamic programming.
Biology review. A genetic sequence is a string formed from a four-letter alphabet {Adenine (A), Thymine (T), Guanine (G), Cytosine (C)} of biological macromolecules referred to together as the DNA bases. A gene is a genetic sequence that contains the information needed to construct a protein. All of your genes taken together are referred to as the human genome, a blueprint for the parts needed to construct the proteins that form your cells. Each new cell produced by your body receives a copy of the genome. This copying process, as well as natural wear and tear, introduces a small number of changes into the sequences of many genes. Among the most common changes are the substitution of one base for another and the deletion of a substring of bases; such changes are generally referred to as point mutations. As a result of these point mutations, the same gene sequenced from closely related organisms will have slight differences.
The problem. Through your research you have found the following sequence of a gene in a previously unstudied organism.
A A C A G T T A C C
What is the function of the protein that this gene encodes? You could begin a series of uninformed experiments in the lab to determine what role this gene plays. However, there is a good chance that it is a variant of a known gene in a previously studied organism. Since biologists and computer scientists have laboriously determined (and published) the genetic sequence of many organisms (including humans), you would like to leverage this information to your advantage. We'll compare the above genetic sequence with one which has already been sequenced and whose function is well understood.
T A A G G T C A
If the two genetic sequences are similar enough, we might expect them to have similar functions. We would like a way to quantify "similar enough."
Edit-distance. In this assignment we will measure the similarity of two genetic sequences by their edit distance, a concept first introduced in the context of coding theory, but which is now widely used in spell checking, speech recognition, plagiarism detection, file revisioning, and computational linguistics. We align the two sequences, but we are permitted to insert gaps in either sequence (e.g., to make them have the same length). We pay a penalty for each gap that we insert and also for each pair of characters that mismatch in the final alignment. Intuitively, these penalties model the relative likeliness of point mutations arising from deletion/insertion and substitution. We produce a numerical score according to the following table, which is widely used in biological applications:
| operation |
cost |
| insert a gap |
2 |
| align two characters that mismatch |
1 |
| align two characters that match |
0 |
Here are two possible alignments of the strings x = "AACAGTTACC" and y = "TAAGGTCA":
x y cost
------------
A T 1
A A 0
C A 1
A G 1
G G 0
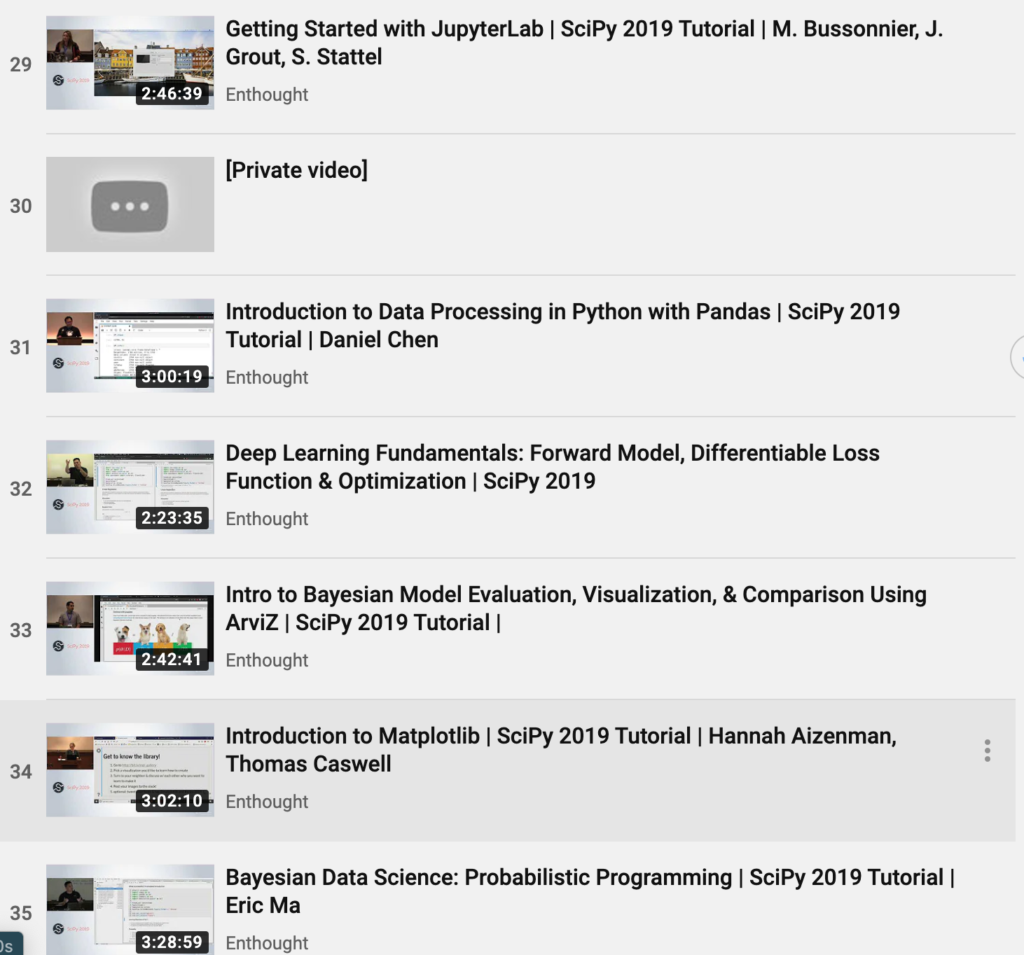
T T 0
T C 1
A A 0
C - 2
C - 2
---
8
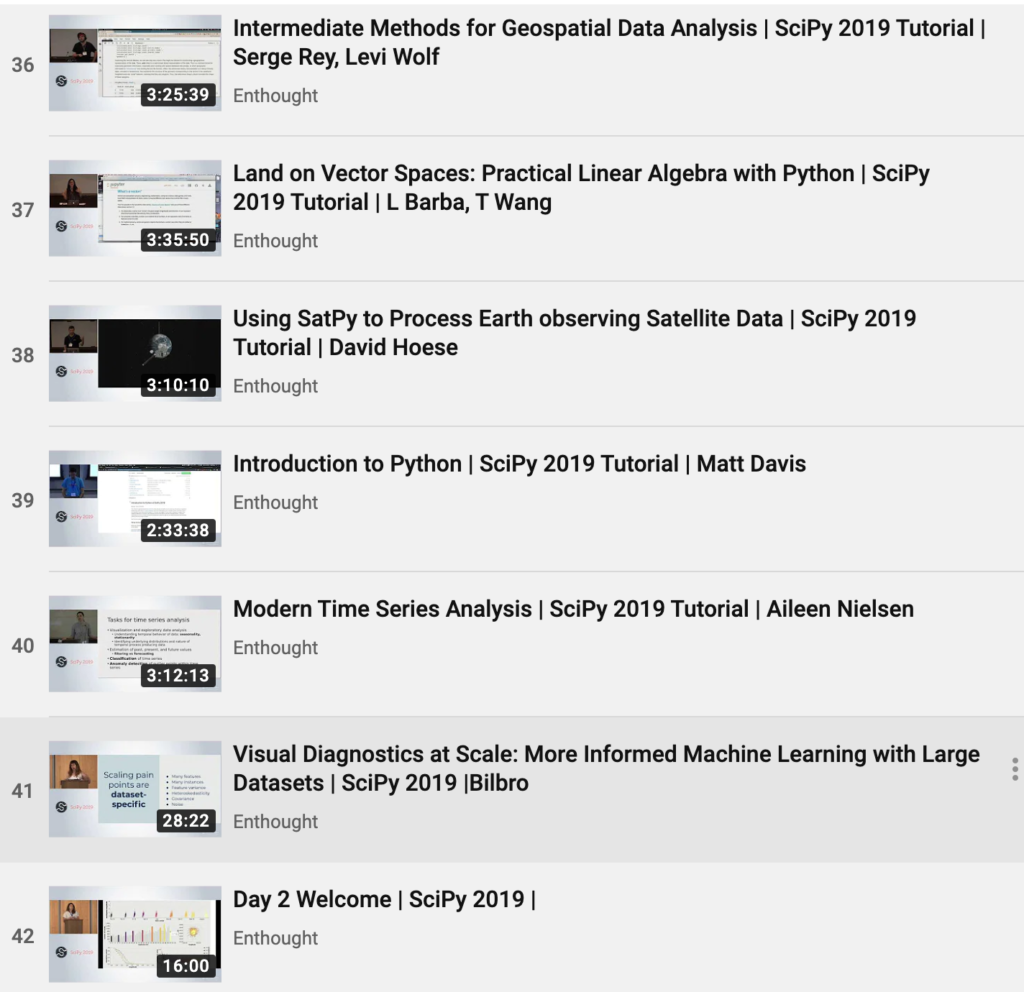
|
|
x y cost
------------
A T 1
A A 0
C - 2
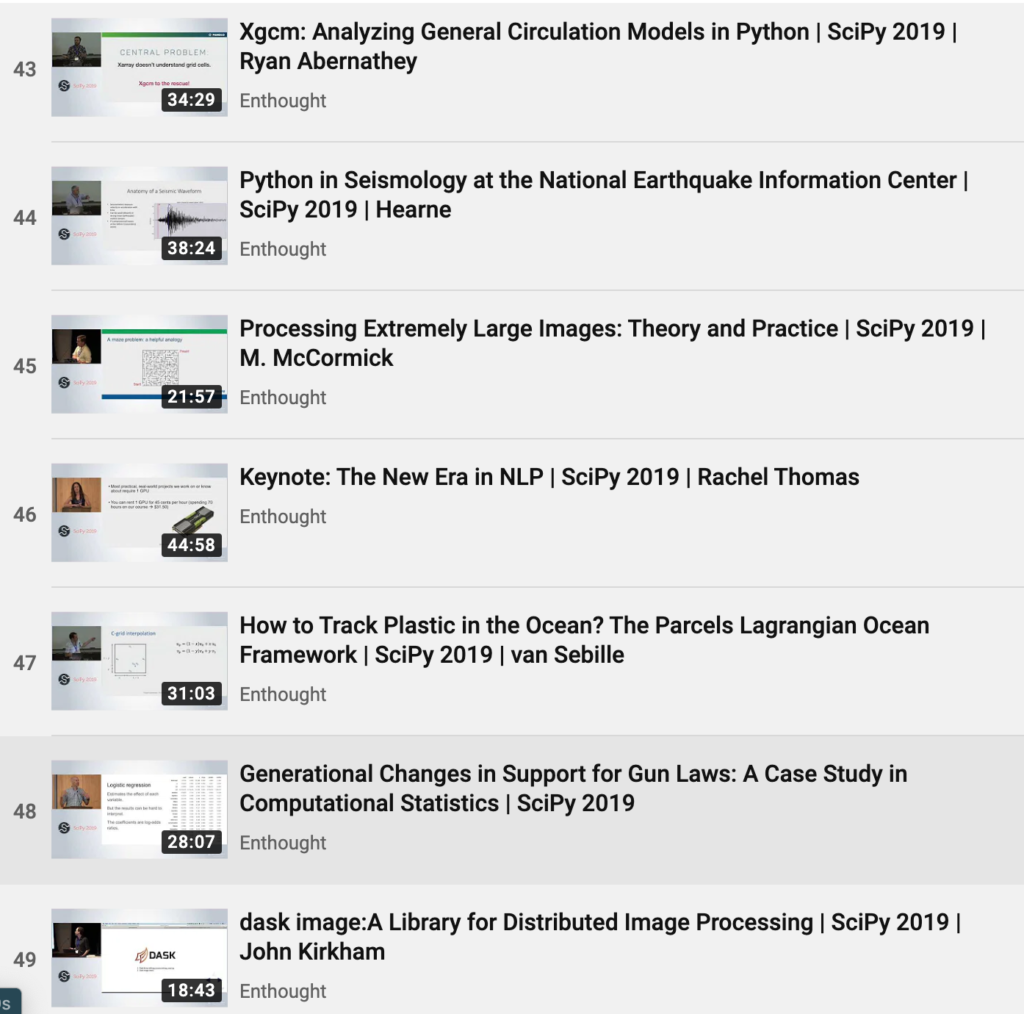
A A 0
G G 0
T G 1
T T 0
A - 2
C C 0
C A 1
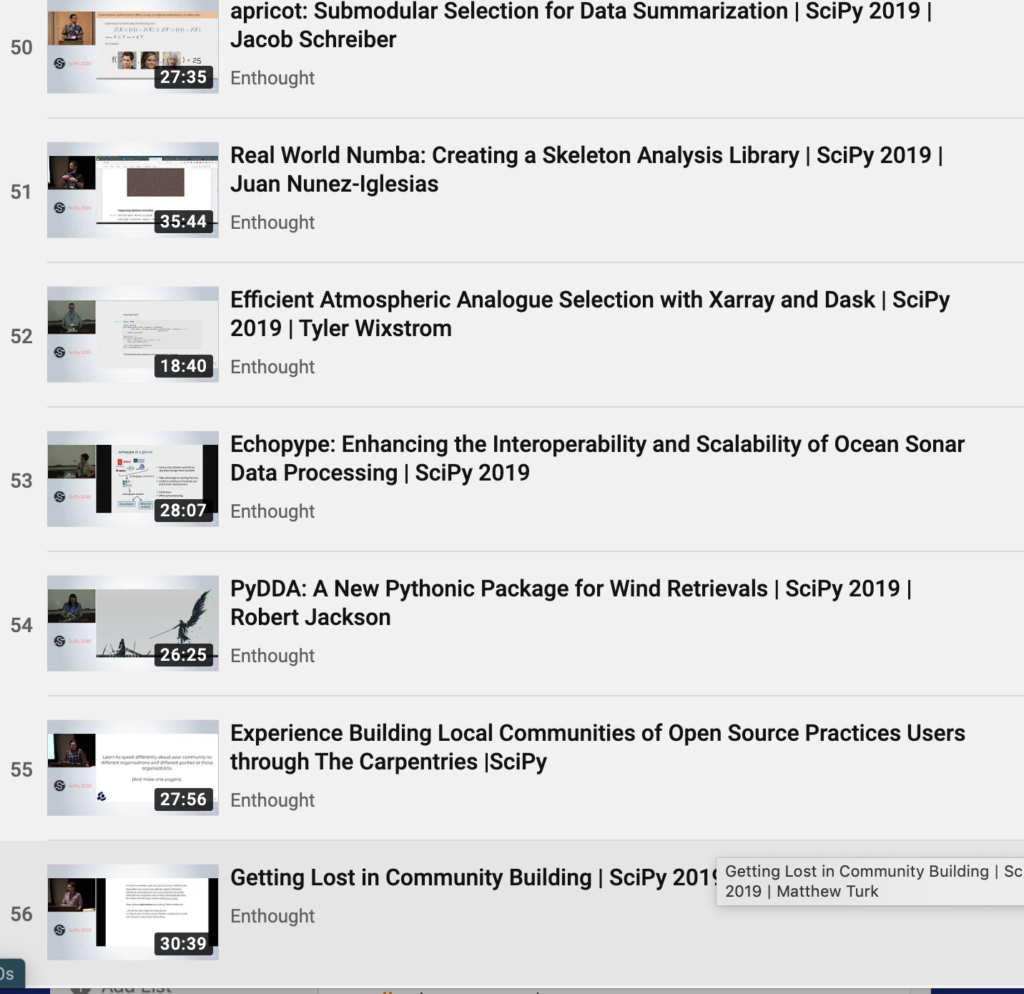
---
7
|
The first alignment has a score of 8, while the second one has a score of 7. The edit-distance is the score of the best possible alignment between the two genetic sequences over all possible alignments. In this example, the second alignment is in fact optimal, so the edit-distance between the two strings is 7. Computing the edit-distance is a nontrivial computational problem because we must find the best alignment among exponentially many possibilities. For example, if both strings are 100 characters long, then there are more than 10^75 possible alignments.
We will explain a recursive solution which is an elegant approach. However it is far too inefficient because it recalculates each subproblem over and over. Once we have defined the recursive definition we can redefine the solution using a dynamic programming approach which calculates each subproblem once.
A recursive solution. We will calculate the edit-distance between the two original strings x and y by solving many edit-distance problems on smaller suffixes of the two strings. We use the notation x[i] to refer to character i of the string. We also use the notation x[i..M] to refer to the suffix of x consisting of the characters x[i], x[i+1], ..., x[M-1]. Finally, we use the notation opt[i][j] to denote the edit distance of x[i..M] and y[j..N]. For example, consider the two strings x = "AACAGTTACC" and y = "TAAGGTCA" of length M = 10 and N = 8, respectively. Then, x[2] is 'C', x[2..M] is "CAGTTACC", and y[8..N] is the empty string. The edit distance of x and y is opt[0][0].
Now we describe a recursive scheme for computing the edit distance of x[i..M] and y[j..N]. Consider the first pair of characters in an optimal alignment of x[i..M] with y[j..N]. There are three possibilities:
- The optimal alignment matches x[i] up with y[j]. In this case, we pay a penalty of either 0 or 1, depending on whether x[i] equals y[j], plus we still need to align x[i+1..M] with y[j+1..N]. What is the best way to do this? This subproblem is exactly the same as the original sequence alignment problem, except that the two inputs are each suffixes of the original inputs. Using our notation, this quantity is opt[i+1][j+1].
- The optimal alignment matches the x[i] up with a gap. In this case, we pay a penalty of 2 for a gap and still need to align x[i+1..M] with y[j..N]. This subproblem is identical to the original sequence alignment problem, except that the first input is a proper suffix of the original input.
- The optimal alignment matches the y[j] up with a gap. In this case, we pay a penalty of 2 for a gap and still need to align x[i..M] with y[j+1..N]. This subproblem is identical to the original sequence alignment problem, except that the second input is a proper suffix of the original input.
The key observation is that all of the resulting subproblems are sequence alignment problems on suffixes of the original inputs. To summarize, we can compute opt[i][j] by taking the minimum of three quantities:
opt[i][j] = min { opt[i+1][j+1] + 0/1, opt[i+1][j] + 2, opt[i][j+1] + 2 }
This equation works assuming i < M and j < N. Aligning an empty string with another string of length k requires inserting k gaps, for a total cost of 2k. Thus, in general we should set opt[M][j] = 2(N-j) and opt[i][N] = 2(M-i). For our example, the final matrix is:
| 0 1 2 3 4 5 6 7 8
x\y | T A A G G T C A -
-----------------------------------
0 A | 7 8 10 12 13 15 16 18 20
1 A | 6 6 8 10 11 13 14 16 18
2 C | 6 5 6 8 9 11 12 14 16
3 A | 7 5 4 6 7 9 11 12 14
4 G | 9 7 5 4 5 7 9 10 12
5 T | 8 8 6 4 4 5 7 8 10
6 T | 9 8 7 5 3 3 5 6 8
7 A | 11 9 7 6 4 2 3 4 6
8 C | 13 11 9 7 5 3 1 3 4
9 C | 14 12 10 8 6 4 2 1 2
10 - | 16 14 12 10 8 6 4 2 0
By examining opt[0][0], we conclude that the edit distance of x and y is 7.
A dynamic programming approach. A direct implementation of the above recursive scheme will work, but it is spectacularly inefficient. If both input strings have N characters, then the number of recursive calls will exceed 2^N. To overcome this performance bug, we use dynamic programming. (Read the first section of Section 9.6 for an introduction to this technique.) Dynamic programming is a powerful algorithmic paradigm, first introduced by Bellman in the context of operations research, and then applied to the alignment of biological sequences by Needleman and Wunsch. Dynamic programming now plays the leading role in many computational problems, including control theory, financial engineering, and bioinformatics, including BLAST (the sequence alignment program almost universally used by molecular biologists in their experimental work). The key idea of dynamic programming is to break up a large computational problem into smaller subproblems, store the answers to those smaller subproblems, and, eventually, use the stored answers to solve the original problem. This avoids recomputing the same quantity over and over again. Instead of using recursion, use a nested loop that calculates opt[i][j] in the right order so that opt[i+1][j+1], opt[i+1][j], and opt[i][j+1] are all computed before we try to compute opt[i][j].
Recovering the alignment itself. The above procedure describes how to compute the edit distance between two strings. We now outline how to recover the optimal alignment itself. The key idea is to retrace the steps of the dynamic programming algorithm backwards, re-discovering the path of choices (highlighted in red in the table above) from opt[0][0] to opt[M][N]. To determine the choice that led to opt[i][j], we consider the three possibilities:
- The optimal alignment matches x[i] up with y[j]. In this case, we must have opt[i][j] = opt[i+1][j+1] if x[i] equals y[j], or opt[i][j] = opt[i+1][j+1] + 1 otherwise.
- The optimal alignment matches x[i] up with a gap. In this case, we must have opt[i][j] = opt[i+1][j] + 2.
- The optimal alignment matches y[j] up with a gap. In this case, we must have opt[i][j] = opt[i][j+1] + 2.
Depending on which of the three cases apply, we move diagonally, down, or right towards opt[M][N], printing out x[i] aligned with y[j] (case 1), x[i] aligned with a gap (case 2), or y[j]aligned with a gap (case 3). In the example above, we know that the first T aligns with the first A because opt[0][0] = opt[1][1] + 1, but opt[0][0] ≠ opt[1][0] + 2 and opt[0][0] ≠ opt[0][1] + 2. The optimal alignment is:
x y cost
------------
A T 1
A A 0
C - 2
A A 0
G G 0
T G 1
T T 0
A - 2
C C 0
C A 1
API specification. Your program EditDistance.java must be organized as a library of static methods with the following API:
public class EditDistance
--------------------------------------------------------------------------------
int penalty(char a, char b) // return the penalty for aligning char a and char b
int min(int a, int b, int c) // return the min of 3 integers
void main(String[] args) // read 2 strings from standard input.
// compute and print the edit distance between them.
// output an optimal alignment and associated penalties.
Your program. Write a program EditDistance.java that reads, from standard input, two strings of characters. (Although, in the application described, the characters represent genetic sequences, your program should handle any sequence of alphanumeric characters.) Your program should then compute and print the edit distance between the two strings. Finally, it should recover the optimal alignment and print it out along with the individual penalties, using the following format:
- The first line should contain the edit distance, preceded by the text "Edit distance = ".
- Each subsequent line should contain a character from the first string, followed by the paired character from the second string, followed by the associated penalty. Use the character '-'to indicate a gap in either string.
Here is a sample execution:
% java-introcs EditDistance < example10.txt
Edit distance = 7
A T 1
A A 0
C - 2
A A 0
G G 0
T G 1
T T 0
A - 2
C C 0
C A 1
The .zip file for this week contains short test data files and actual genomic data files, as well as the readme.txt for this assignment (recall the unzipping instructions here). Or, you can use thesequence directory course ftp site.
Be sure to test thoroughly using the short test files and the longer actual data files. Also, make up a short test file of your own and describe it in your readme.txt file.
Analysis. After you have tested your program using not only the example provided above, but also the many short test data files in the sequence subdirectory, it is time to analyze its running time and memory usage. Using the genomic data sets referred to in the readme.txt file, use the doubling method to estimate the running time (in seconds) of your program as a function of the lengths of the two input strings M and N. For simplicity, assume M = N in your analysis. Also analyze the memory usage (in bytes). Be sure to enter these results in your readme and answer all the questions.
See the checklist for information about giving Java more memory and running timing tests.
Submission. One partner should submit the files EditDistance.java and readme.txt (including the analysis and test data you created). If you are partnering, the second partner should only submit this abbreviated partner readme.txt.
This assignment was created by Thomas Clarke, Robert Sedgewick, Scott Vafai and Kevin Wayne.
Copyright © 2002.