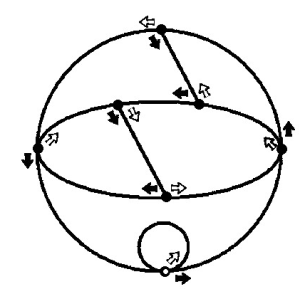
My guest blogger is David Wilson, a fellow fan of sequences. It is a nice exercise to understand how this graph works. When you do, you will discover that you can use this graph to calculate the remainders of numbers modulo 7. Back to David Wilson:

I have attached a picture of a graph.

Write down a number n. Start at the small white node at the bottom of the graph. For each digit d in n, follow d black arrows in a succession, and as you move from one digit to the next, follow 1 white arrow.

For example, if n = 325, follow 3 black arrows, then 1 white arrow, then 2 black arrows, then 1 white arrow, and finally 5 black arrows.

If you end up back at the white node, n is divisible by 7.

Nothing earth-shattering, but I was pleased that the graph was planar.

Tanya Khovanova's Math Blog

Mathematics, applications of mathematics to life in general, and my life as a mathematician.